HGS RESEARCH HIGHLIGHT – Finite-volume flux reconstruction and semi-analytical particle tracking on triangular prisms for finite-element-type models of variably-saturated flow
Selzer, P., Allgeier, J., Therrien, R., & Cirpka, O.A. (2021). Finite-volume flux reconstruction and semi-analytical particle tracking on triangular prisms for finite-element-type models of variably-saturated flow. In Advances in Water Resources (Vol. 154, p. 103944). https://doi.org/10.1016/j.advwatres.2021.103944
CLICK HERE TO READ THE ARTICLE.
A recent article co-authored by Aquanty co-founder René Therrien and researchers at the University of Tübingen (Germany) introduces a novel postprocessing method to generate conforming velocity fields, which are element-wise mass conservative and feature a continuous normal flux component on element boundaries. Based on this, semi-analytical particle tracking methods on deformed triangular prisms are derived and implemented in analogy to Pollock’s method. This means no particle trajectory exits at an unphysical location or just aborts unexpectedly somewhere in the domain. Finally, there is a fast and robust technique available for particle tracking for finite-element type models of variably saturated flow in porous media without significant numerical artifacts. The simulation framework is linked to HydroGeoSphere as an external post-processing tool and is readily available for users!
Figure 1: Application of the finite-volume flux reconstruction to the catchment scale. Comparison of the hydraulic head field of the primal finite-element type solution at the top of the domain (a) and at the bottom of the domain (c) with the results for the finite-volume flux reconstruction at the top of the domain (b) and at the bottom (d), respectively. At the top flow is in general unsaturated whereas at the bottom flow is saturated everywhere.
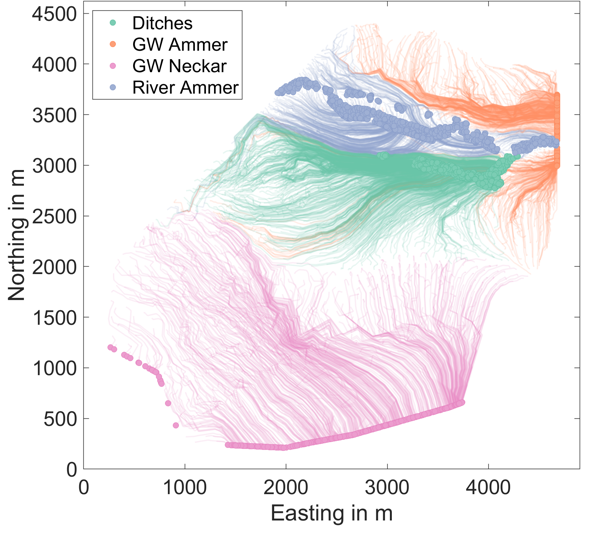
Figure 2: Trajectories of particles, which are released at the top of the domain and tracked until they reach an outlet boundary. Possible ending locations are drainage channels (green), the Ammer river (blue), groundwater outflow within the Ammer valley (orange), or groundwater outflow in the Neckar valley (purple).
Are you interested in this new semi-analytical particle tracking method? Then check out the source code on GitHub (https://github.com/PhilippSelzer/FluxCorr_ParticleTracking) or mail the corresponding author Philipp Selzer (philipp.selzer@gmx.net) to get a run through of the methods and the code!
Abstract:
Consistent particle tracking relies on conforming velocity fields that ensure local mass conservation on elements. Cell-centered finite-volume and mixed finite-element methods result in conforming velocity fields but this is not the case for continuous Galerkin methods, such as the standard finite element method (FEM). Nonetheless standard FEM is often used for subsurface flow modeling because it yields a continuous approximation of hydraulic heads, and it naturally handles unstructured grids and full material tensors. Acknowledging these advantages and the wide-spread use of finite-element-type simulations, we present a postprocessing method that reconstructs a cell-centered finite-volume solution from a finite-element-type solution of the variably-saturated subsurface flow equation to obtain conforming, mass-conservative fluxes. Using the linear average velocity field derived from these fluid fluxes, we employ element-wise analytical solutions for triangular prisms to compute particle trajectories and associated travel times. As a result, we can compute consistent particle trajectories for variably-saturated flow solutions generated by node-centered methods, such as finite element or finite difference methods, that do not yield conforming velocity fields. Our flux reconstruction solves a linear elliptic problem whose size is on the order of the number of elements, which is computationally much faster than solving the initial, non-linear transient variably-saturated flow equation. Compared to other postprocessing schemes, our flux reconstruction is numerically stable, fast to compute, and does not induce severe numerical artifacts when applied to heterogeneous domains with strongly varying velocities. However, these advantages come with a comparably high coding effort and the necessity of solving a global system of equations. We show that the results of our flux reconstruction are close to the node-centered primal solution for variably saturated three-dimensional flow with heterogeneous material properties.